第二章  误差与分析数据的处理

 

第一节  定量分析误差

掌握：误差的类型

      准确度与精密度

      有效数字的意义记录、修约及运算规则

熟悉：提高分析结果准确度的方法

      有效数字在定量分析中的应用

了解：可疑值的取舍、显著性检验

      分析结果的表示方法

定量分析的任务是要准确地解决“量”的问题，但是定量分析中的误差是客观存在的，因此，必须寻找产生误差的原因并设法减免，从而提高分析结果的可靠程度，另外还要对实验数据进行科学的处理，写出合乎要求的分析报告。

一、误差的类型

    1. 系统误差（可定误差）

       由某种确定的原因引起，一般有固定的方向，大小在试样间是恒定的，重复测定时重复出现。

       按系统误差的来源分类：方法误差、仪器或试剂误差、操作误差。

       方法误差：滴定分析反应进行不完全、干扰离子的影响、滴定终点与化学计量点不符、副反应的发生、沉淀的溶解、共沉淀现象、灼烧时沉淀的分解或挥发。

       仪器或试剂误差：砝码、容量器皿刻度不准、试剂中含有被测物质或干扰物质。

       操作误差：称样时未注意防止吸湿、洗涤沉淀过分或不充分、辨别颜色偏深（浅）、读数偏高（低）。

       按系统误差的数值变化规律分类：恒定误差、比例误差。

       系统误差可用加校正值的方法予以消除。

2. 偶然误差（随机误差、不可定误差）

       由于偶然的原因如温度、湿度波动、仪器的微小变化、对各份试样处理时的微小差别等引起，其大小和正负都不固定。

       偶然误差服从统计规律，可用增加平行测定次数加以减免。

二、准确度和精密度

    1. 准确度与误差

      准确度表示分析结果与真实值接近的程度。准确度的大小用绝对误差或相对误差表示。评价一个分析方法的准确度常用加样回收率衡量。

    （1）绝对误差

       测量值与真实值之差称为绝对误差。d = x - m

（2）相对误差

       绝对误差与真值的比值称为相对误差。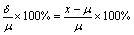

       若真实值未知，但d 已知，也可表示为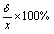

    （3）真值与标准参考物质

       理论真值：如某化合物的理论组成等。

       约定真值：如国际计量大会上确定的长度、质量、物质的量单位等。

       相对真值：如标准参考物质的含量。

       标准参考物质：经权威机构鉴定并给予证书的，又称标准试样。

       实际工作中，常把最有经验的人用最可靠的方法对标准试样进行多次测定所得结果的平均值作为真值的替代值。

 2. 精密度与偏差

      精密度表示平行测量的各测量值之间互相接近的程度。精密度的大小可用偏差、相对平均偏差、标准偏差和相对标准偏差表示。重复性与再现性是精密度的常见别名。

      偏差：d = x_i - 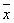              平均偏差：

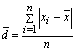
      相对平均偏差：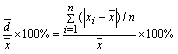

      标准偏差（标准差）：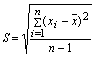

      相对标准偏差（变异系数）：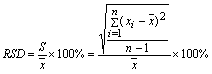

      实际工作中多用RSD表示分析结果的精密度。

3. 准确度与精密度的关系

  精密度是保证准确度的前提条件。只有在消除了系统误差的情况下，才可用精密度表示准确度。

三、提高分析结果准确度的方法

（1）选择恰当的分析方法

（2）减小测量误差

 

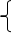  称量误差：称样量＞0.2g，才能使称量相对误差＜0.1%

滴定管读数误差：消耗滴定剂体积＞20ml，才能使滴定相对误差＜0.1%

 （3）减少测量中的系统误差

校准仪器、对照试验、加样回收试验、空白试验

（4）减小测量中的偶然误差

增加平行测定次数

 

第二节  有效数字及其应用

一、有效数字

    指实际能测量到的数字，只允许数据的末位数欠准。

    保留有效数字位数的原则：

（1）1~9均为有效数字，0既可以是有效数字，也可以作定位用的无效数字；

（2）变换单位时，有效数字的位数不变

（3）首位是8或9时，有效数字可多计一位

（4）pH、lgK或pK_a等对数值，有效数字仅取决于小数部分数字的位数；

（5）常量分析一般要求四位有效数字，以表明分析结果的准确度为1‰。

二、有效数字的记录、修约及运算法则

1、记录

2、有效数字修约规则

（1）四舍六入五留双；如3.35、3.25、3.152

（2）不能分次修约；如3.1462

（3）运算过程中可先多保留一位有效数字；

（4）修约的结果应使准确度的估计值变差；

（5）在作统计检验时，标准偏差可多保留1~2位参加运算，计算结果的统计量可多保留一位数字与临界值比较；

（6）表示标准偏差和RSD时，通常取一位有效数字即可，最多取二位。

3、有效数字运算法则

加减运算，有效数字以小数点后位数最少的数据为准；

乘除运算，有效数字以有效数字位数最少的数据为准。

三、有效数字在定量分析中的应用

1.正确选择测量仪器

2.正确记录测量数据

3.正确表示分析结果

 

第三节  定量分析结果的处理

一、可疑数据的取舍

    1. Q检验法

（1） 数据排列   X₁  X₂  ……  X_n 

      （2） 求极差 X_n - X₁ 

      （3） 求可疑数据与相邻数据之差

               X_n - X_n-1   或  X₂ -X₁

      （4） 计算：

 Q =      若Q＞QP, n  则舍弃。

     2. G检验法

（1）排序：X₁  X₂  ……  X_n

（2）求包括异常值在内的平均值和标准偏差s

（3）计算G值：

            G = 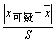      若G＞G_{n, a}   则舍弃。

二、分析结果的表示方法

t分布

    无限多次的测量值的偶然误差分布服从正态分布，而有限量测量值的偶然误差的分布服从t分布。t分布曲线的纵坐标是概率密度，横坐标是统计量t（t =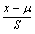，m为真实值或总体均值，S为样本标准差，仿照u =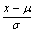，s为总体标准差），分布曲线随自由度f（f = n-1）而改变，当f趋近∞时，t分布就趋近正态分布。

置信水平：测量值落在（m ± tS）内的概率，以P表示，又称置信度。

显著性水平：a =1 -P

不同f值及概率所相应的t（t_{a, f}）值见表2-5。

（一）一般对于常规或验证性试验

1、对试样平行测定3次

2、计算相对平均偏差

3、若 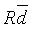      ≤0.2%认为符合要求，取平均值    为测量结果

否则，此次实验不符合要求，需重做。

（二）分析结果的统计处理方法

无限次数测量的偶然误差的分布——正态

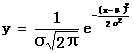      分布曲线（高斯曲线）

数学表达式：

 

1、偶然误差的正态分布

（1）x=μ，y最大，体现测量值的集中趋势

（2）以x=μ对称，正负误差出现的概率相等

（3）说明小误差出现的概率大，大误差出

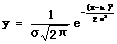          现的概率小

数学表达式：

2、平均值的精密度

              

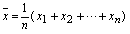
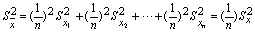
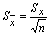           一般平行测定3~4次即可。

3. 平均值的置信区间

  置信区间：在一定的置信水平时，以测定结果为中心，包括总体均值在内的可信范围，称为置信区间。

  有限次测量可按下式计算平均值的置信区间：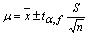

  置信区间分为双侧置信区间与单侧置信区间两种。

三、显著性检验

    1. F检验（精密度显著性检验）

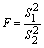       （S₁ >S₂）  若F > F_{a, f1, f2} ，则两组数据的精密度存在显著性差异。

2. t检验

      （1）样本平均值与标准值的t检验（准确度显著性检验）

         检验目的：分析结果是否正确或新分析方法是否可用。

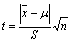              若t ³ t_{a, f} ，则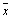与m 间存在显著性差异。

     （2） 两个样本均值的t检验

         检验目的：两个操作者、两种分析方法或两台仪器的分析结果是否存在显著性差别；不同分析时间的样品是否存在显著性变化；两个样品中某成分的含量是否存在显著性差别。

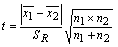                S_R 为合并标准差，总自由度f = n₁+ n₂-2

          

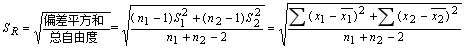
          若t ³ t_{a, f} ，则两组数据的平均值存在显著性差异。

      3. 几点说明

      （1）先进行F检验再进行t检验；

      （2）F检验用单侧检验，t检验有单侧检验和双侧检验之分；

      （3）一般取a = 0.05，P = 0.95。